A Convenient Formula for Bicycle Spoke Length

Bicycle spoke lacing patterns exist for many reasons from aesthetic to functional. I present a parameterized formula for determining the necessary spoke length given typical measures of a bicycle wheel. First the problem is assessed for simplifying assumptions and symmetry. Next, a solution for the spoke length is derived in a minimally complex case, and finally a short analysis of the results is conducted.

Symmetry and Simplifications

In practice bicycle spokes work in concert with many other parts of the bicycle. For example the spokes may account for any difference in spacing on either side of a hub so that the rim and tire remain centered within the fork or stays. In other cases one may find bicycle wheels with non-uniform spacing between spokes. Common to all these special cases, however, is the lowly spoke – the single ray from hub to rim – which is to be the primary subject of this study. Once the length of a spoke can be determined in general the effort required to repeat this for some combination of special cases is relatively small.

Our analysis will deal only with the features of the system which matter directly – the size and location of the hub, the rim, and the spoke. Other consequences of reality (a domain better suited for engineers) such as offsets, depths, deflections, etc, will be assumed to be negligible.

Derivation

Represent the hub and the rim as two circles in parallel planes separated by a height h. Assume that the circles centers both lie on a line normal to the planes. We designate r and R as the radii of the hub and rim respectively and note that r <= R. A line segment, representing the spoke, emanates from the hub and terminates on the rim.

Further analysis will ignore the height between the hub and the rim and consider only the in-plane projection of the spoke. Applying the Pythagorean theorem with the height and the in-plane spoke length easily recovers the true spoke length.

Define the angle which the spoke forms with a coincident radius of the hub as θ such that when that angle is zero the spoke is a continuation of the radius.

Notice now the beauty of the arrangement. As described the spoke will always lie along a chord of the rim, and that chord will always contain a chord of the hub. These chords are denoted C_R and c_r and they are both situated a distance d from the center. Clearly, then, the length of the spoke is simply half of the difference between the two chords. This remains true even when the spoke angle θ exceeds 90 degrees. Using θ and the hub radius r gives d and the spoke length s follows.

Now the interesting part is out of the way. Returning to the world of three dimensions we can simply add the effect of the height h back into the spoke. Because the height is orthogonal to the other measurements we can simply use the sum of squares formula to find s_3, the true spoke length in three dimensions.

It’s not a pretty equation, and I have little interest in further simplification. In my book as long as I can enter the formula into a graphing calculator and turn the knobs then we’re golden. In the next section we will analyze the expression for s using an interactive graphing calculator.

Analysis

Desmos Graph

The expression for s immediately passes some sanity checks, namely that when the spoke lies along the radius (θ = 0) its length is s = R - r and that when the spoke runs the opposite direction (θ = π) its length is s = R + r.

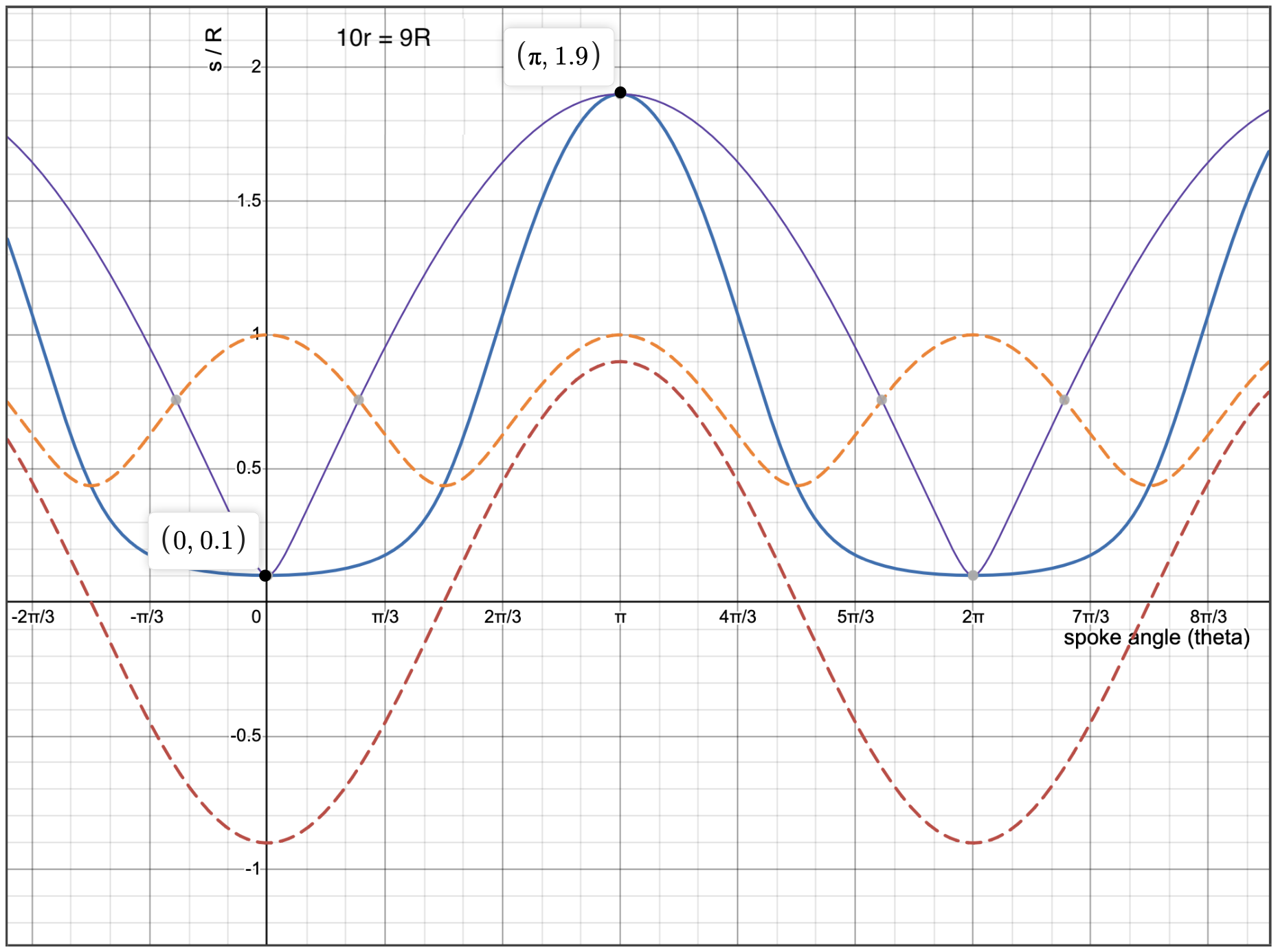
How can we think of the terms in this formula? I was tempted by the apparent simplicity of the term - r cos(θ) to see it as the primary driver of s and to see the more complicated term as an error correction term of sorts. After a more careful inspection it became apparent just how far off base that picture is.

In most cases R is significantly larger than r and the root term is dominated by the size of R^2. Again this checks with our sense of reality – the spoke length tends toward R as r -> 0. What happens, then, when r is close to R?

Let’s consider another scenario where r = R = u. In this case the left hand term can be reduced to something that appears to be the absolute value of the term on the right hand side.

This is a particularly interesting result and validates the model in yet another scenario. If the hub were the same size as the rim then the spoke length is zero until the angle exceeds 90 degrees – that is until the spoke falls below the local “horizon” of the hub. All of this has fallen out of our formula thanks to the fact that it transforms into a difference between the cosine term and its absolute value when r = R. This was enough to convince me that there is a special relationship between the two terms much more interesting than one being dominant and the other being an error correction.

My familiarity with these functions is not really strong enough to clear the way for further insights, but I am sure they exist.

Before we conclude I’d like to point out yet another beautiful aspect of this formula; its simplicity. There are other ways to frame the problem and they naturally lead to different ways to solve for the spoke length. One other method is to think of the angle of the spoke as being formed by beginning with the hub and rim aligned, so that the spoke is a radius, and then turning the hub around its center through the angle phi. Keeping the ends of the spoke affixed to the rim and the hub would require that the spoke be made of elastic or that the thought experimenter have a very strong mind. The expression for s that this setup produces is as follows:

I’ve left the expression in a form which makes its origins in simple trigonometry very clear. This expression lines up with our first in the trivial points (phi = 0 and phi = pi) and it covers the whole range of s. In every sense it is just as correct as the first expression for s but it is less intuitive because ψ != θ. As you turn the hub by angle ψ in your mind there is some transfer function to θ which, at first, seems to be direct thanks to small angles. For larger angles this is not true and ψ and θ diverge. For a bicycle builder, who cares about θ, the first function is much more useful.

Conclusion

Having added to our toolbox a convenient form for the spoke length s for a wheel with rim and hub radii R and r respectively given the spoke off-radial angle θ we are now free to compose wheels with any number of interesting spoke patterns. Left so far undiscussed are any additional concerns for the practical construction of such designs.